AA UE 0

Ex_AdvAlg_00-0.pdf

1

Antwort (falsch)

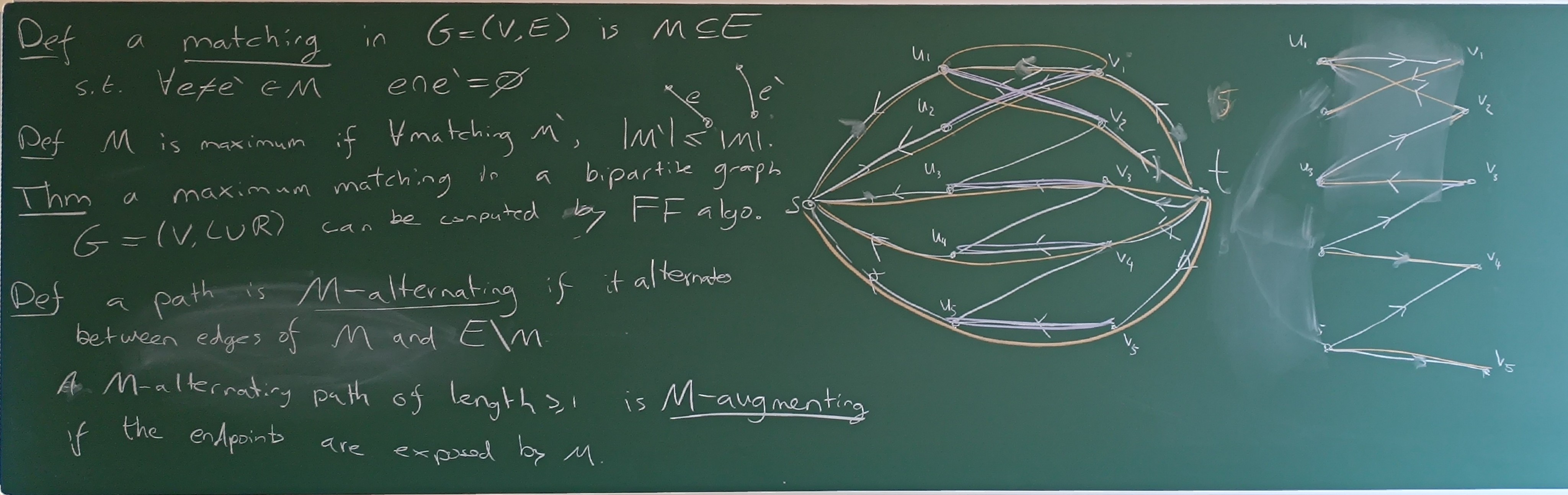
Given $G=\{V,E\}$ which is bipartite
compute maximum matching
via Reduction to maximum flow

$V_1{V}_2$ are the two sides of the Graph
Construct new Graph $G^{\prime }=\{V\cup \{s,t\},E\cup \{(s,a)|a\in V_1\}\cup \{(a,t)|a\in V_2\}\}$
All edges in $G^{\prime }$ have a capacity of 1
Compute maximum s-t-flow in G’
The maxmum matching in G are all Edges $E_{matching}=\{(a,b)|c((a,b));(a,b)\in E^{\prime }\}$

2

Antwort

If there is no augmenting path there is either no exposed vertecies
or there is no path from s to a exposed v vertex.
If there is a exposed v vertecx all the edges of the vertex either to a u vertex that is already in a matching. (Because there is no path from s to the exposed vertex)

If the matching is not maximun there must be an exposed vertex w
If there

3

The path has an odd length

If the path is of length 1 the vertex at position 2 must be an exposed node
For every vertex v at position n where n is odd the
The vertex must be in a matching with the next vertex
For every vertex u at position n where n is even
The next vertex can not be in a matching because the u is
Therefore the path must have edges that are alternating in the matching and are not
The first and last edge can not be in the matching bacuse they have an exposed node.
Therefore the path must have one more edge that is in the matching then not in the matching.