Advanced Algorithms UE 3

by Maarten Behn
Group 5

Exercise 3.1 (Uniqueness in Tutte-Berge Formula?)

Can there be several minimizers $U$ in the Tutte-Berge Formula?
Either give an example with several sets $U$ achieving the minimum, or prove that the set U is unique.

Yes. The formula involves taking a minimum over all subsets $U\subseteq V$.
There can be more that one Subset that yield the same value and are both minimal.

Example

Let $G$ be a path on 2 vertices: $v1-v2$
Max matching is 1 (match $v1v2$​​)

Go over all possible $U\subseteq V$:

$U=\varnothing$:

$G-\varnothing =G$ is connected and even.
$\to o(G-U)=0$
Formula: ​$(|V|+|U|-o(G-U))/2=(2+0-0)/2=1$

$U=\{v1\}$:

$G-\{v1\}=\{v2\}$
$\to$ one part left, $v2$ (odd)
$\to o(G-U)=1$
Formula: ​$(|V|+|U|-o(G-U))/2=(2+1-1)/2=1$

$U=\{v2\}$:

$G-\{v2\}=\{v1\}$
$\to$ one part left, $v1$ (odd)
$\to o(G-U)=1$
Formula: ​$(|V|+|U|-o(G-U))/2=(2+1-1)/2=1$

$U=\{v1,v2\}$:

$G-\{v1,v2\}=\varnothing$
$\to o(G-U)=0$
Formula: ​$(|V|+|U|-o(G-U))/2=(2+2-0)/2=2$

$U=\varnothing$, $U=\{v1\}$, $U=\{v2\}$ all yield 1 and are therefore all minimum.

Exercise 3.2 (Edmonds-Gallai Decomposition)

Compute the Edmonds-Gallai Decomposition of the following graph.

Compute even, odd and free Vertecies

Transclude of AA-UE-3.2.excalidraw

Move G in representation seen in lecture.

This is not part of the Algorithm. I only change how the G is drawn.

Transclude of AA-UE-3.2.2.excalidraw

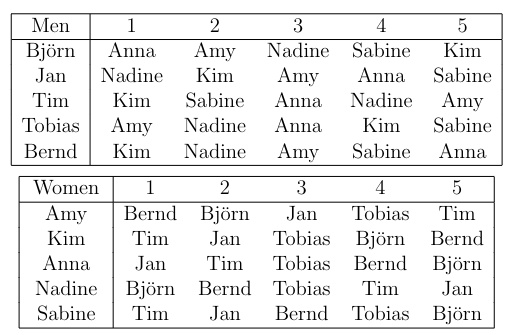
Exercise 3.3 (Stable Matchings)

We are given the following preference list.

Find a stable matching with the Gale Shapley Algorithm.
Do this for both cases: First, in the case that the men propose to the women.
Second, in the case that the women propose to the men. Compare the two results.
Which one is optimal for the women? Why?

Perform Gale-Shapley Algorithm

Transclude of AA-UE-3.3.excalidraw

Results

Transclude of AA-UE-3.3-result.excalidraw

This result shows that the Woman gernally get a better result when they propose.
Sabiene is an exception here, just because it happens that the first preference of each of the other Woman (Tim, Jan, Bernd), prefer them (Kim, Anna, Nadine) over Sabiene.

The Gale-Shapley Algorithm computes the optimal stable match for the subset that propses.
The other subset gets an arbitrary match.

For exmaple:
When the Men propose and the first preference of each Man is disjunkt,
the preference of the Woman is not regarded.
Each Woman is just propsed to once.
This men could be the one least preferred.