{
"rule": {
"conditions": {
"all": [{
"fact": "file",
"path": "$.tags",
"operator": "regexMatch",
"value": "uni/Mat3"
}]
},
"event": {
"type": "match"
}
}
} Q 6b3mq
Definition überabzählbar
? 73vt
Definition
Eine Menge heißt überabzählbar, wenn sie nicht abzählbar ist. Dabei heißt eine Menge abzählbar, wenn sie entweder endlich ist oder eine Bijektion zur Menge der natürlichen Zahlen existiert. Eine Menge ist also genau dann überabzählbar, wenn ihre Mächtigkeit (entspricht der Anzahl der Elemente bei endlichen Mengen) größer ist als die der Menge der natürlichen Zahlen.
Q 3cpl1
Definition Wahrscheinlichkeitsraum
? 7l7i
Definition
Das Tripel heißt ein Wahrscheinlichkeitsraum.
Ist höchstens abzählbar, so heißt ein diskreter Wahrscheinlichkeitsraum.
Ist Überabzählbar, so heißt ein stetiger Wahrscheinlichkeitsraum.
Q 7nb1t
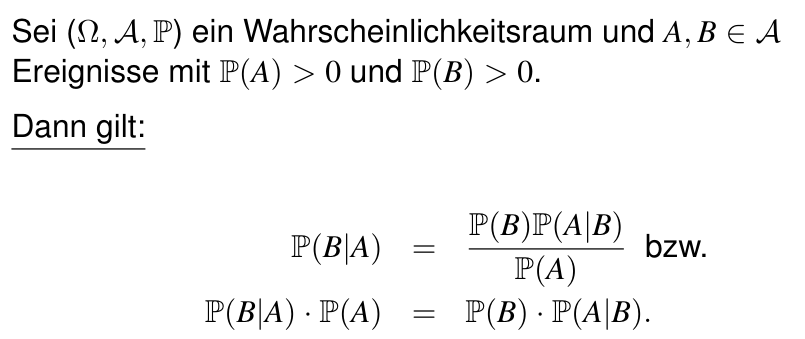
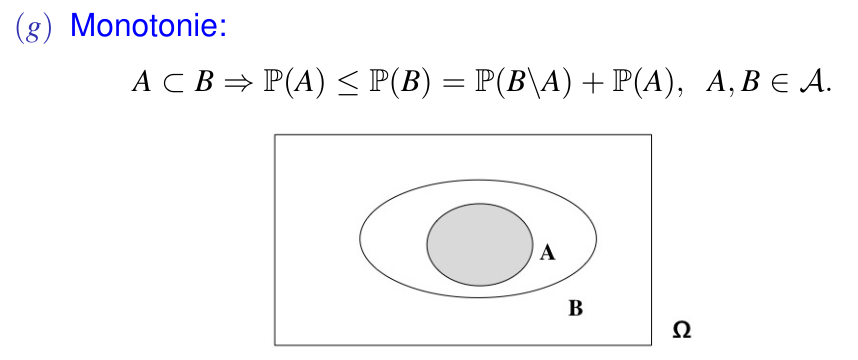
Was sagt Monotonie über Wahrscheinlichkeitsmaße aus?
? 505p
Q 1i5tu
und sind stochastisch abhängig
? 2ij9
Q 2gqus
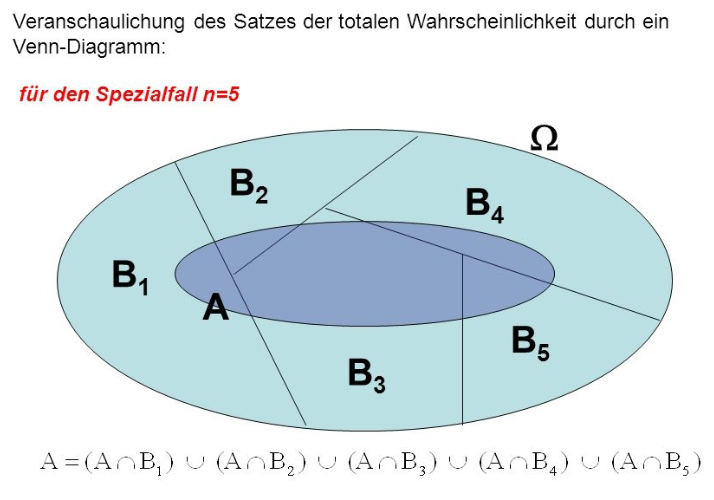
Satz von der totalen Wahrscheinlichkeit
? 16kv
Q 4c0vr
Stochastische Unabhängigkeit von Ereignissen
? z182

Q 65upm
Definition Wahrscheinlichkeitsfunktion
? 2k9n

Q 2q6rs
Definition Diskrete Gleichverteilung (La Place)
? 6mqo
-
-
Alle Ereignisse gleiche Wahrscheinlichkeit
-
Bsp.: Fairer Würfelwurf, zufällige Auswahlen, Lotto
m_{k} := \mathbb{E}[X^{k}]
#Q #AOSR/aila5 Wie errechnet man das k-te zentrale Moment ? #AOSR/aila5/m/5erm\mu_{k} := \mathbb{E}\left[(X - \mathbb{E}[X])^{k}\right]
#Q #AOSR/13c3u Wie errechnet man das k-te zentrale Moment empirisch? ? #AOSR/13c3u/m/4nsg\mu_{k} = \frac{1}{n} \sum_{i=1}^n (x_i - \overline x)
#Q #AOSR/3p1r4 Wie errechnet man das k-te absolute Moment ? #AOSR/3p1r4/m/z405M_{k} := \mathbb{E}\left[|X|^{k} \right]
#Q #AOSR/74qca Wie errechnet man $Var(X)$ vom [[Erwartungswert]] $\mathbb{E}[X]$ ? #AOSR/74qca/m/3mdeVar(X) = \mathbb{E}[X^{2}] - \mathbb{E}^{2}[X]
#Q #AOSR/7iuff Im welchen Verhältnis steht Varianz und Momente? ? #AOSR/7iuff/m/4e43 $Var(X)$ = 2 te zentrale Moment $\mu_{k} := \mathbb{E}\left[(X - \mathbb{E})^{2}\right] = \mathbb{E}[X^{2}] - \mathbb{E}^{2}[X]$ #Q #AOSR/66mql Wie errechnet man $Var(X)$ empirisch? ? #AOSR/66mql/m/3gb5 $$Var(X) = \frac{1}{n} \sum_{i=1}^n (x_i - \overline x)^2$$ #Q #AOSR/u5p5p Wie errechnet man $\overline{x}$ empirisch? ? #AOSR/u5p5p/m/1h7k $$\overline{x} = \frac{1}{n} \sum\limits_{i=1}^{n} x_{i}$$ #Q #AOSR/2hf9d Wie errechnet man die [[Standardabweichung]]? ? #AOSR/2hf9d/m/6s12SD(X) := \sqrt{Var(X)}
#Q #AOSR/4bin0 Wie errechnet man die [[Standardabweichung]] empirisch? ? #AOSR/4bin0/m/6kod\text{SD}(X) = \sqrt{\frac{1}{(n-1)}\sum\limits_{i}(x_{i}-\overline{x})^{2}}
#Q #AOSR/517k0 Wie errechnet man die Schiefe? ? #AOSR/517k0/m/3u5p\begin{align}
v(X)
&= \frac{\text{3 te zentrale Moment}}{\text{Standartabweichung}^{3}} \
&= \frac{\mu_{3}(X)}{SD(X)^{3}}
= \frac{\mu_{3}(X)}{Var(X)^{\frac{2}{3}}}
= \frac{\mu_{3}(X)}{\mu_{2}(X)^{\frac{2}{3}}} \
&= \frac{\mathbb{E}[X^{3}] - 3\mathbb{E}[X] \cdot \mathbb{E}[X^{2}] + \mathbb{E}[X]^{3}}{(\mathbb{E}[X^{2}] - \mathbb{E}^{2}[X])^\frac{2}{3}} \
& \text{oder} \
&= \mathbb{E}[X^{3}] \left(\frac{X - \mathbb{E}[X]}{SD(X)}\right)
\end{align}
v_{e}(x) = \frac
{\frac{1}{n} \sum_{i}(x_{i} - \overline{x})^{3}}
{(\frac{1}{n} \sum_{i}(x_{i} - \overline{x})^{2})^{3/2}}
\begin{align}
w(X)
&= \frac{\text{4 te zentrale Moment}}{\text{Standartabweichung}^{4}} \
&= \frac{\mu_{4}(X)}{SD(X)^{4}}
= \frac{\mu_{4}(X)}{Var(X)^{\frac{1}{2}}}
= \frac{\mu_{4}(X)}{\mu_{2}(X)^{\frac{1}{2}}} \
& \text{oder} \
&= \mathbb{E}[X^{4}] \left(\frac{X - \mathbb{E}[X]}{SD(X)}\right)
\end{align}
w_{e}(x) = \frac
{\frac{1}{n} \sum_{i}(x_{i} - \overline{x})^{3}}
{(\frac{1}{n} \sum_{i}(x_{i} - \overline{x})^{2})^2}
Cov(X, Y) = \mathbb{E}[X \cdot Y] - \mathbb{E}[X] \cdot \mathbb{E}[Y]
![[Kovarianz von zwei Zufallsvariablen-1749985113653-0.png|800x291]] #Q #AOSR/6l93q Wie errechnet man Korrelationskoeffizient? ? #AOSR/6l93q/m/gufb\rho(X,Y) = \frac{Cov(X, Y)}{\sqrt{Var(X) Var(Y)}} \in [-1, 1]
#Q #AOSR/7g670 Was ist $Cov(X, X) =$::$Var(X)$ #AOSR/7g670/s/6t41 #Q #AOSR/4js3i Ist $Cov(X, Y) = Cov(Y, X)$?::Ja #AOSR/4js3i/s/70cb #Q #AOSR/pk8e5 Was ist $Cov(a + X, b + Y) =$::$Cov(X, Y)$ #AOSR/pk8e5/s/3ioa #Q #AOSR/erq94 Was ist $Cov(X, Y + Z) =$::$Cov(X, Y) + Cov(X, Z)$ #AOSR/erq94/s/46ik Was ist $Cov(X + Z, Y) =$::$Cov(X, Y) + Cov(Z, Y)$ #AOSR/erq94/s/3v30 #Q #AOSR/1qmj2 Was ist $\mathbb{E}[X \cdot Y] =$::$\mathbb{E}[X] \cdot \mathbb{E}[Y] + Cov(X, Y)$ #AOSR/1qmj2/s/2kaq #Q #AOSR/ndmvc Was ist $Var(X \pm Y) =$::$Var(X) + Var(Y) \pm 2 \cdot Cov(X, Y)$ #AOSR/ndmvc/s/3h8a #Q #AOSR/2uhgd Was gilt für die Kovarianz wenn $X$ und $Y$ stochastisch unabhängig sind? ? #AOSR/2uhgd/m/6ktk $Cov(X, Y) = 0$ #Q #AOSR/7md70 Sind $X$ und $Y$ [[stochastische unabhängigkeit]] wenn $Cov(X, Y) = 0$ ist? ? #AOSR/7md70/m/1f0c Nein #Q #AOSR/5oe8k Was ist [[Die Quantilsfunktion]]? ? #AOSR/5oe8k/m/3qs2 ![[Die Quantilsfunktion-1749985943304-0.png|800x407]] #Q #AOSR/1stq7 Was ist die [[Bernoulli-Verteilung]]? ? #AOSR/1stq7/m/7p0m Es gibt ein $p \in [0, 1]$ und $X \in \{1, 0\}$ $\mathbb{P}(X = 1) = p$ und $\mathbb{P}(X = 0) = 1 - p$ #Q #AOSR/4i1a9 Was ist die [[Binomialverteilung]]? ? #AOSR/4i1a9/m/38ma Parameter $n$ und $p$f_{X}(x |n, p) = \mathbb{P}(X = x) = \binom{n}{x} \cdot p^{x} \cdot (1 - p)^{n - x}
für $x \in \{0, 1, ..., n \}$ $x$ Erfolge von $n$ unabhängigen Experimenten #Q Was ist die [[Poisson-Verteilung]]?f_{Possion}(k|\lambda) = \frac{\lambda^{k}}{k!} e^{-\lambda}
Anzahl der Ereignisse im festen Zeit- oder Raumbereich, Ereignisse sind unabhängig und mit konstanter Rate $\lambda = n \cdot p$ #Q #AOSR/3057i Was ist das Verhältnis der [[Binomialverteilung]] zur [[Poisson-Verteilung]]? ? #AOSR/3057i/m/5ojt Wenn $n\longrightarrow \infty, \space \space p \longrightarrow 0$ dann $n \cdot p = \lambda$ #Q #AOSR/4qgf1 Was ist die verallgemeinerte Geometische Verteilung? ? #AOSR/4qgf1/m/e4gq $$f(r,j) = (1-p)^{j-r} \cdot p^r \cdot \binom{j-1}{r-1} \space , \space \space r \in \mathbb{N}, \space j \geq r$$ Der $r$-te Treffer in $j$-Versuchen #Q #AOSR/5ipb0 Wie lautet die [[Gauß'sche Normalverteilung]]? ? #AOSR/5ipb0/m/1l98 $$f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{- \frac{1}{2}(\frac{x- \mu}{\sigma})^2}$$ für $x\in \mathbb R$  #Q #AOSR/2oj53 Was ist das Verhältnis der [[Poisson-Verteilung]] zur [[Gauß'sche Normalverteilung]]? ? #AOSR/2oj53/m/39fs Ab $\lambda = 30 \space \space \sim N(\mu = \lambda, \sigma^2 = \lambda)$ #Q #AOSR/7gejh Wie funktioniert der [[Plug-in Schätzer]]? ? #AOSR/7gejh/m/407b Schätz einen Parameter $\theta$ aus empirisch Warscheinlichkeiten. z.B. $p_{1}(\theta), p_{2}(\theta), p_{3}(\theta)$ gegeben und wir nutzen die Anahme das:\hat{p}{1} = \frac{N{1}}{n}
; \hat{p}{2} = \frac{N{2}}{n}
; \hat{p}{3} = \frac{N{3}}{n}
L(y, \theta) = \log(Z(y, \theta)) = \sum\limits_{i=1}^{n} log(p(y_{i}, \theta))
L(y, \theta) = n \cdot log(2) - n \cdot log(\theta) + \sum\limits_{i=1}^{n} log(y_{i}) + \frac{-1}{\theta} \sum\limits_{i=1}^{n} y_{i}^{2}
vereinfachen. Dann nach $\theta$ ableiten und gleich $0$ setzen.\frac{d ; L(y,\gamma)}{d ; \theta} = -\frac{n}{\theta} + \frac{1}{\theta^{2}} \sum\limits_{i=1}^{n} y_{i}^{2} = 0
und nach $\theta$ umstellen. #Q #AOSR/4s7us Was ist eine [[Stetige Gleichverteilung]]? ? #AOSR/4s7us/m/4acl ![[Stetige Warscheinlichkeitsverteilung-1747033367990-0.png|800x437]] #Q #AOSR/3mcdu Wie funktioniert der [[Neyman-Pearson-Test]]? ? #AOSR/3mcdu/m/6uuf ![[Neyman-Pearson-Test-1753557873509-0.png|800x491]] #Q #AOSR/1bon0 Wie funktioniert der [[Binomialtest]]? ? #AOSR/1bon0/m/l07p ## Vorraussetzungen - Ja, Nein Ergebnis - $n$ unabhängige Versuche - Du kennst den theoretische Verteilung $p$ ## Hypothesen - $H_{0}: p = p_{0}$ und - $H_{1}: p \neq p_{0}$ (zweiseitig) - $H_{1}: p > p_{0} \vee p < p_{0}$ (einseitig) ## [[Binomialverteilung]] berrechen $$\mathbb{P}(X = x) = \binom{n}{x} \cdot p^{x} \cdot (1 - p)^{n - x}$$ ## [[p-Wert]] berrechen ### zweiseitig $$\text{p-Wert}=\mathbb{P}(X \leq x) + \mathbb{P}(X \geq (n−x))$$ ### einseitig $$\text{p-Wert}=\mathbb{P}(X \leq x)$$ oder $$\text{p-Wert}=\mathbb{P}(X \geq x)$$ ## Test verworfen wenn $\text{p-Wert} < a$ z.B. $a = 0.05$ #Q #AOSR/3oqvh Wie funktioniert der t-Test? ? #AOSR/3oqvh/m/7kks ## Vorraussetzungen - **metrisch skalierte Daten** (z. B. Größen, Punkte, Gewichte) - Die Daten sind **annähernd normalverteilt** (wichtig bei kleinen Stichproben) - Du kennst **nicht** die Populationsstandardabweichung → deshalb der **t-Test** (nicht z-Test) ## Berrechen - $X \sim N(\mu_x, \sigma ^2_x), \space Y \sim N(\mu_y, \sigma^2_y)$ - $\sigma^2_x = \sigma^2_y, \space H_0: \mu_1 = \mu_2\\ \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space H_1: \mu_1 \neq \mu_2$ - Einstichproben t-Test: - linksseitig: $H_0: \mu \geq \mu_0$, $H_1: \mu < \mu_0$ - rechtsseitig: $H_0: \mu \leq \mu_0$, $H_1: \mu > \mu_0$ - zweiseitig: $H_0 : \mu = x$, $H_1: \mu \neq x$ - Teststatistik: $T=\frac{\overline x - \mu_0}{\frac{s}{\sqrt n}}$ - Nachschlagen in der t-Verteilungstabelle, wobei $Freiheitsgrad = n-1$. - Ablesen des kritischen Wertes: - rechtsseitig: direkt ablesbar - linksseitig: Kehrwert bilden (einfach ein “$-$” davor) - beidseitig: Signifikanzniveau halbieren (z.B. bei $5\%$ zu $\alpha = 0,025$) und zwei Kritische Werte bilden, einmal normal ablesen und dann für den anderen Kehrwert bilden - Verwerfen wenn: - links: $\text{t-Wert} < \text{Kritischer Wert}$ - rechts: $\text{t-Wert} > \text{Kritischer Wert}$ - beidseitig: $\text{t-Wert} \notin (\text{Kritischer Wert }_1 , \text{ Kritischer Wert}_2)$ #Q #AOSR/7pg7t Wie funktioniert der [[Chi-Quadrat–Unabhängigkeitstest]]? ? #AOSR/7pg7t/m/2b1h ## Voraussetzungen: - nominales oder ordinales Skalenniveau - zufallsverteilt ## Berrechen - $x^2 = \sum \frac{(\text{beobachtete Häufigkeit } - \text{ erwartete Häufigkeit})^2}{\text{erwartete Häufigkeit}}$ - Häufigkeit $f_e = \frac{\text{Zeilensumme } \cdot \text{ Spaltensumme}}{\text{Stichprobengröße}}$  - Kritischen Wert in Tabelle ablesen mit Hilfe von $(1-\alpha)$ und Freiheitsgrad $df = (\text{Anzahl der Spalten }-1) \cdot (\text{Anzahl der Zeilen} -1)$ - Wenn $x^2 > \text{ Kritischer Wert}$ dann gibt es einen statistisch signifikanten Zusammenhang. - $H_0$: $X$ und $Y$ sind stochastisch unabhängig - $H_1$: Zwischen $X$ und $Y$ gibt es einen statistisch signifikanten Zusammenhang #Q #AOSR/1e330 Was kann man mit dem Fallzahlabschätzung machen? ? #AOSR/1e330/m/5ag1 **Notwendige Stichprobengröße** (also die "Fallzahl") für eine geplante Studie berechnen. Du planst einen t-Test für zwei Gruppen (z. B. Placebo vs. Medikament) und gibst an: - α = 0,05 (Fehlerwahrscheinlichkeit) - Power = 0,80 (also 80 % Chance, einen vorhandenen Effekt zu entdecken) - Effektgröße d = 0,5 (mittlerer Effekt laut Cohen) Das ergibt eine nötige Fallzahl von ca. **64 Personen pro Gruppe** (insgesamt 128). #Q #AOSR/2gtou\frac{d}{da} a \cdot log(b) = ?
? #AOSR/2gtou/m/4i9q\frac{d}{da} a \cdot log(b) = \frac{a}{b}
#Q #AOSR/8m540\frac{d}{da} log(a) = ?
? #AOSR/8m540/m/e76b\frac{d}{da} log(a) = \frac{1}{a}
#Q #AOSR/5ah11\frac{d}{da} log(1 - a) = ?
? #AOSR/5ah11/m/2hsm\frac{d}{da} log(1 - a) = \frac{-1}{1-a}
#Q #AOSR/6ugmu\log \left( \prod_{i=1}^{n} y_{i} \right) = ?
? #AOSR/6ugmu/m/7hga\log \left( \prod_{i=1}^{n} y_{i} \right) = \sum\limits_{i=1}^{n} y_{i}