Türme von Hanoi

20221028_TH_M1-Skript_v02-0.pdf

Das folgende Spiel wurde 1883 von Édouard Lucas erfunden. Gegeben sind drei Stäbe ($A,B,C)$ zum stapeln und eine Anzahl von $n$ gelochte Scheiben, die zu Beginn alle auf dem Stab A gelegt sind.

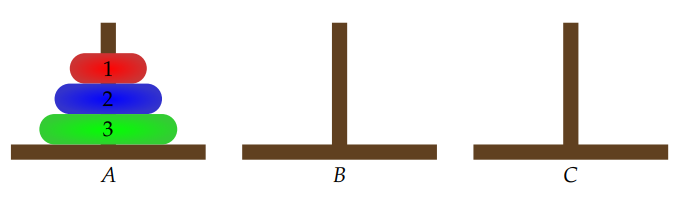
Dabei sind die Scheiben alle unterschiedlich groß und zu Beginn der Größe nach geordnet (die größte unten, die kleinste oben). Aufgabe ist es nun, die Scheiben von Stab A auf den Stab C zu legen.

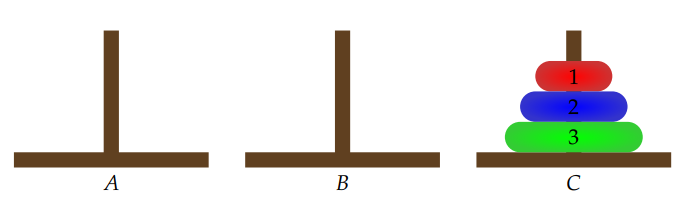
• Es darf nur eine Scheibe auf einmal bewegt werden.
• Eine Scheibe darf nur auf einen leeren Platz, oder auf eine größere Scheibe gelegt werden.

Behauptung: Es gibt einen Algorithmus, der die Aufgabe für jedes $n\in \mathbb{N}$ löst.

Bei $n=0$ ist nichts zu tun.

Daher Induktionsanfang: $n=1$
Bewege die eine Scheibe von $A$ nach $C$.

Induktionschrintt
Geben sei also ein Algorithmus, der die Aufgabe für $n$ Scheiben löst. Wir müssen nun zeigen, dass es einen Algorithmus für $n+1$ Scheiben gibt, der die Aufrgabe löst.

Nach Induktionsvoraussetzung wissen wir, dass es einen Algorithmus für $n$ Scheiben gibt. Nutze diesen um die oberen $n$ Scheiben von $A$ nach $B$ zu bewegen.
Bewege dann die $(n+1)$-te Scheibe von $A$ nach $C$.
Nutze nun wieder den Algorithmus für $n$ Scheiben um die $n$ Scheiben von $B$ nach $C$ zu bewegen.

Offensichtlich kann man mittels vollständige Induktion nicht nur beweisen, dass bestimmte Algorithmen korreckt sind, sondern auch rekusive Algorithmen entwerfen.