THI2 Probeklausur

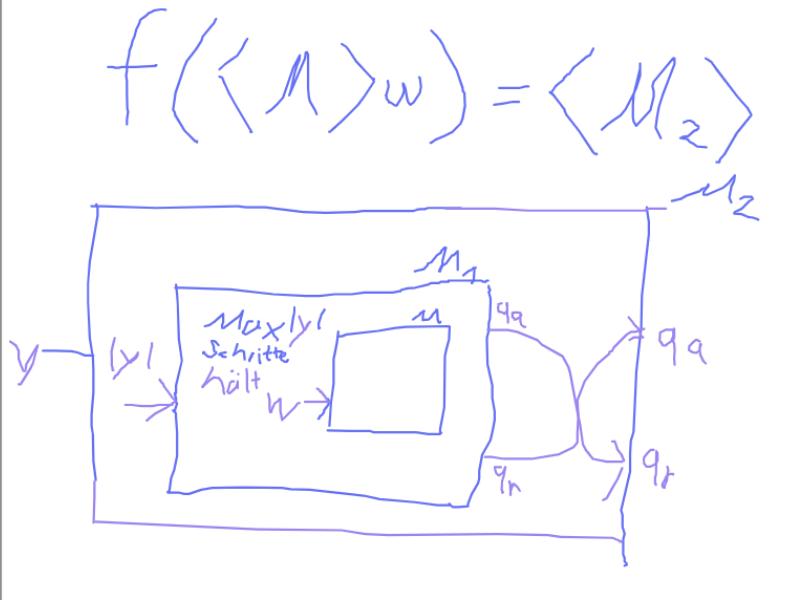
1.

a)

Nein da dieser Satz gilt:

Damit $L$ entscheidbar ist muss $\overline{L}$ auch semi entscheidbar sein.

b)

Ist wahr da $A$ $L$ entscheidet, hält A auf allen eingaben Wörten von ${\Sigma }^{\ast }$. Somit hält auch $A$ auf allen Wörtern von $\overline{L}$.
Das tauschen der Endzustände ändert nichts daran welche Wörter $A$ erkennt.
Daher erkennt (und entscheidet sogar) alle Wörter von $\overline{L}$.

c)

Ja denn:

Sei $f:{\Sigma }^{\ast }\to {\Sigma }^{\ast }$
und $g:{\Sigma }^{\ast }\to {\Sigma }^{\ast }$
gilt
$L\le L^{\prime }:=\forall w\in L⟺f(w)\in L^{\prime }$
$L^{\prime }\le L^{\prime \prime }:=\forall w\in L^{\prime }⟺g(w)\in L^{\prime \prime }$
daher
$L\le L^{\prime \prime }:=\forall w\in L⟺g(f(w))\in L^{\prime \prime }$

d)

Nein da wir dieses Lemma hatten:

e)

Nein denn aus diesen beiden Sätzen:

Bildet sich dieses Korollar

Also muss auch $\overline{L}$ von einer Grammatik erzeugt werden damit $L$ entscheidbar ist.

2

a)

b)

Ein Entscheidungsproblem ist ein Problem was nur ja oder nein zurück gibt.
Wortproblem = Entscheidungsproblem ob ein Wort in der Sprache ist.

Ein Entscheidungsproblem ist semi-entscheidbar wenn es nur ja aber nicht nein zurück geben kann.
Halteproblem = semi-entscheidbares Wortproblem

c)

Die Chomsky-Hierarchy

	Name	Grammatik	Sprache	äquivalent
Typ 0		Jede		Turing Maschine
Typ 1	monoton	$w⟶u\Vert w\Vert \le \Vert u\Vert$		linear beschränkte NTM
Typ 2	Kontextfreie Grammatik	$A⟶w$	Kontextfreie Sprache	Kellerautomat
Typ 3	rechtslinear	$A⟶u$ oder $A⟶uB$	Reguläre Sprache	DEA, NEA, ε-NEA, wort-NEA

siehe:
Sprachklasse

Link to original

3

a) + b)

Ich gehe mal davon aus das ein loop nicht bei jeder iteration wieder $x_1$ abfragt. denn dann würde das Programm nicht halten.

0: $x_1=3,x_2=27$
1: loop 3 mal
3: 2: nach loop: $x_1=24$
4: $x_3=3$
5: $x_3=3$ ist falsch ⇒ if wird übersprungen
8: $x_3=27$
⇒ $f(3,27)=27$

c)

Kann vereinfacht dargestellt werden als:
if $x_1^{x_1}\ge x_2$ then $x_3=x_1$ else $x_3=x_2$ end

Wenn der loop durch eine while Schleife ersetzt wird das Programm nur terminieren wenn $x_1=0$ ist und $x_3=x_2$ sein. 

4

Mann kann eine Turing Maschine (DTM) für das Problem bauen.

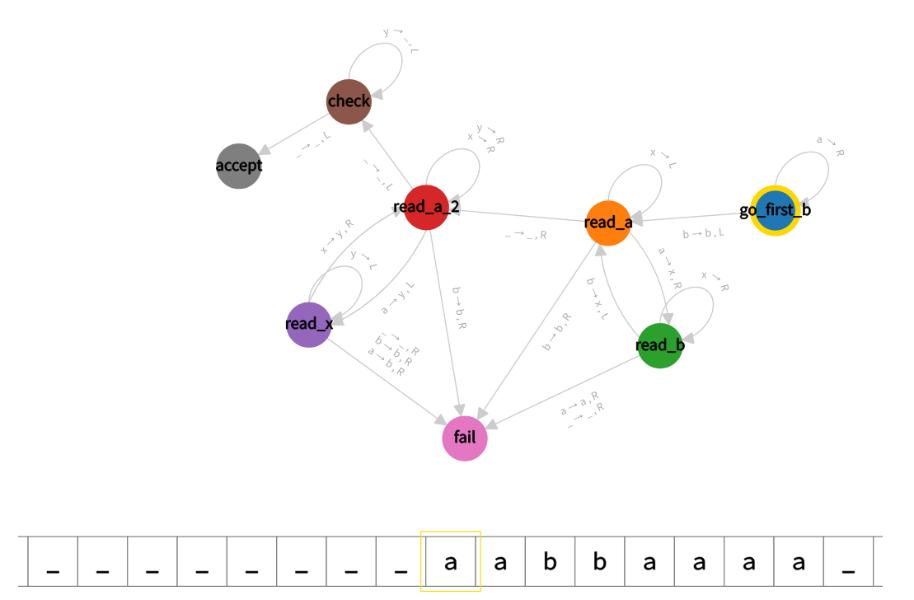
input: 'aabbaaaa'  
blank: '_'  
start state: go_first_b  
table:  
  go_first_b:   
    a: R  
    b: {write: b, L: read_a}  
  read_a:  
    a: {write: x, R: read_b}  
    x: L  
    b: {write: b, R: fail}  
    _: {write: '_', R: read_a_2}  
  read_b:  
    b: {write: x, L: read_a}  
    x: R  
    a: {write: a, R: fail}  
    _: {write: '_', R: fail}  
  read_a_2:  
    a: {write: y, L: read_x}  
    x: R  
    y: R  
    _: {write: '_', L: check}  
    b: {write: b, R: fail}  
  read_x:  
    x: {write: y, R: read_a_2}  
    y: L  
    a: {write: b, R: fail}  
    b: {write: b, R: fail}  
    _: {write: '_', R: fail}  
      
  check:  
    y: {write: '_', L: check}  
    _: {write: '_', L: accept}  
      
  fail:  
  accept:   

Daher ist die Sprache laut Chomsky-Hierarchy mindest Typ 1
Jede Grammatik von einem höheren Typ ist auch vom Typ 1

5

Semi entscheidbar

Sätze und Lemma aus der Vorlesung:
Das Halteproblem ist semi entschidbar.
Das Halteproblem ist nicht entschidbar.
Wenn $L_1\le L_2$ dann:
$L_2$ semi entschidbar $\Rightarrow$ $L_1$ semi entscheidbar
Wenn $L_1{\le }_T{L}_2$ dann:
$L_1$ nicht entschidbar $\Rightarrow$ $L_2$ nicht entscheidbar

$H_{\epsilon }=\{<M>|\text{M ist TM und ha¨lt auf }\epsilon \}$

$H_{\epsilon }\le H$:
$f(<M>)=<M>\epsilon$
wobei $M$ eine TM ist die auf $\epsilon$ hält.

Da $H_{\epsilon }\le H$ gilt ist $H_{\epsilon }$ semi entscheidbar.

$H\le H_{\epsilon }$:
Mann bekommt M und w und soll nun eine Maschine M’ bauen die genau dann hält wenn M auf w hält.
$M^{\prime }$ ist eine Maschine die $<M>w$ als Maschine reinbekommt sie hält wenn M auf w hält und gibt accept zurück.
Wenn M nicht auf w hält dann hält auch M’ nicht.

Satz von Rice Versuch (nicht richtig)

Aus der Vorlesung:
Satz von Rice:
Jede nichttriviale semantische Eigenschaft einer TM ist unentschidbar.

$H_{\epsilon }$ ist nichttriviale da es gibt:
P is not trivial when $\exists M,M^{\prime }$ with $M\in P$ and $M\notin P$
$M_{all}$ die Turing Maschine die auf allen Wörtern hält, hält auch auf $\epsilon$.
$M_{none}$ die Turing Maschine die auf keinem Wort hält, hält auch nicht auf $\epsilon$.

$H_{\epsilon }$ ist semantische da die Eigenschaft das $M$ auf $\epsilon$ hält impliziert, dass
P is semantik if $\forall M,M^{\prime }$ with $L(M)=L(M^{\prime })$ then $M\in P⟺M^{\prime }\in P$
Es gibt

Bonus

$\overline{H}\le P$
$P:=\{(L(M)|\text{M ist TM und L(M) ist unendlich})\}$