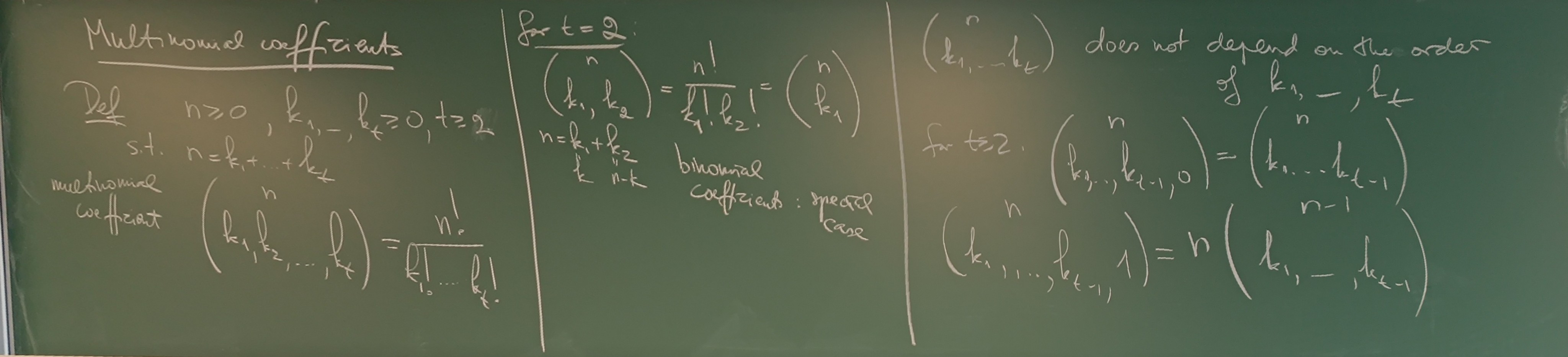DisMat Lernzettel

Graph

• Graph isomorphism Self-complementary graph

• regular Graph
  A Graph is called regular if all vertices have the same Valency.

  • vollstädiger Graph $K_n$

  • Cycle Graph $C_n$

  • vollständiger Bipartiter Graph $K_{n,m}$

• vollstädiger Graph
  $K_n=\{V,E\}$
  $V:=\{v_1,...,v_n\}$
  $E:=\{\{v_i,v_j\}:1\le i\le j\le n\}$
  $|E|=\left(\genfrac{}{}{0ex}{}{n}{2}\right)=\frac{n(n-1)}{2}$

• Handschaking Lemma
  In einem einfachen ungerichteten Graph:
  Die Menge der Knoten mit ungerader Grad ist gerade.

$$\sum _{v\in V}deg(v)=2|E|$$

• Durchmesser eines Graph
  max(min(path)) in G

• Euler characteristic
  $V-E+F=2$

• Eulertour

• Hamilton Kreis

• Network Flow and Max Flow Problem

Enumarative combinatorics

Prroving stuff

• combinatorial identities

• Double counting

multinomial coeffcients

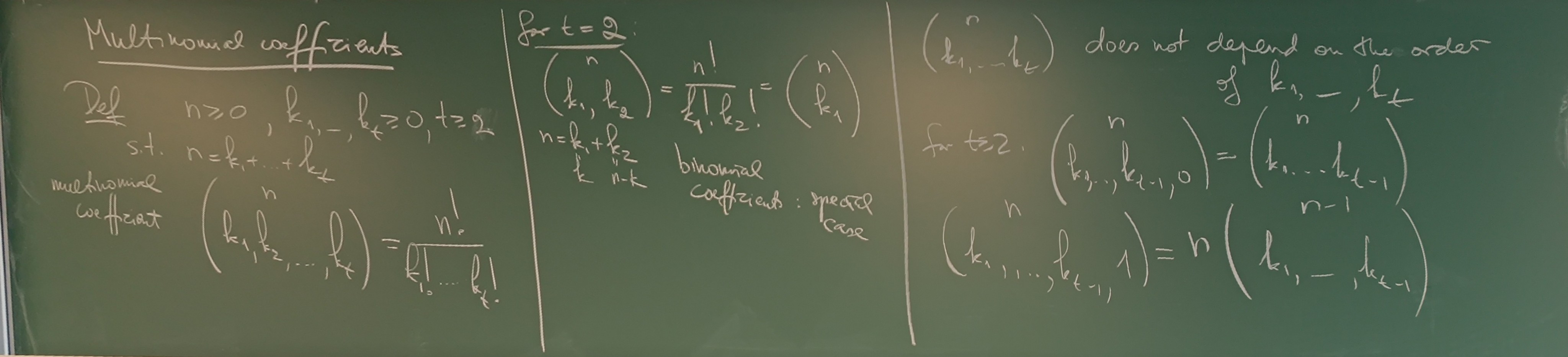
Link to original

multinomial therom

$$(x_1+x_2+...+x_t{)}^n=\sum _{k_1+k_2+...+k_t=n}(\genfrac{}{}{0ex}{}{n}{k_1,k_2,...,k_t})\cdot x_1^{k_1}\cdot x_2^{k_2}\cdot ...\cdot x_t^{k_t}$$

• Vandermodes identity

$$\left(\genfrac{}{}{0ex}{}{m+n}{r}\right)=\sum _{k=0}^r\left(\genfrac{}{}{0ex}{}{m}{k}\right)\left(\genfrac{}{}{0ex}{}{n}{r-k}\right)$$

• Proof of Lucas

$$\left(\genfrac{}{}{0ex}{}{(...,n_1,n_0{)}_p}{(...,k_1,k_0{)}_p}\right)\equiv \left(\genfrac{}{}{0ex}{}{(...,n_2,n_1{)}_p}{(...,k_2,k_1{)}_p}\right)\left(\genfrac{}{}{0ex}{}{n_0}{k_0}\right)\equiv ...\equiv \prod \left(\genfrac{}{}{0ex}{}{n_i}{k_i}\right)$$ $$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\prod \left(\genfrac{}{}{0ex}{}{n}{k}\right)mod2$$

• Inklusion-Exklusion
  Seien $A_1,...,A_k$ endliche Mengen. Dann gilt:

| A_{1} \cup \cdots \cup A_{k}| = \\ & + |A_{1}| + \cdots +|A_{k}| \\ & - |A_{1} \cap A_{2}| - |A_{1} \cap A_{3}| - ... \\ & + |A_{1} \cap A_{2} \cap A_{3}| + |A_{1} \cap A_{2} \cap A_{4}| + ... \\ & ... \end{split}

• Derangeemt

$$d_n=n!(\frac{1}{0!}-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+...+(-1{)}^n\frac{1}{n!})$$

Rekursive Reihen

• Fibunacci Numbers
  $F_0=F_1=1$
  $F_n=F_{n-1}+F_{n-2}$

• Falling Factorial
  $(n{)}_k=x!(\genfrac{}{}{0ex}{}{n}{k})\frac{n!}{(n-k)!}$

• Stirling Numbers First Kind

$$s(n+1,k)=ns(n,k)+s(n-2,k-1)$$

• unsigned Stirling Numbers First Kind

$$\tilde{s}(n,k):=(-1{)}^{n-k}s(n,k)=|s(n,k)|$$

• Stirling Numbers Second Kind

$$S(n+1,k)=kS(n,k)+S(n,k-1)$$ $$S(n,0)=\{\begin{array}{ll}0& \text{if }n\ne 0\\ 1& \text{if }n=0\end{array}$$ $$S(n,k)=0\text{ if }k>n$$ $$S(n,k)=\frac{1}{k!}\sum _{j<1}^k(-1{)}^{k-j}(\genfrac{}{}{0ex}{}{k}{j})\cdot j^n$$

• Bell numbers

$$B_n=\sum _{k=0}^{n}S(n,k)$$

• Ordered Bell Numbers

$${\hat{B}}_n=\sum _{k=0}^{n}k!S(n,k)$$

• Counting sujektions

$$\alpha (n,k)=\sum _{j=1}^k(-1{)}^{k-j}(\genfrac{}{}{0ex}{}{k}{j})j^n$$