THI2 Lernzettel

Turing Maschine

Definition

$M=(Q,\Sigma ,\Gamma ,[,\delta ,q_s,q_a,q_r)$
$Q$ endliche Menge an Zuständen
$\Sigma$ das Eingabealphabet
$\Gamma$ das Arbeitsalphabet
$[\in \Gamma \backslash \Sigma$ der linke Endmarker
$\text{textvisiblespace}\in \Gamma \backslash \Sigma$ das Blanksymbol
$\delta :Q\times \Gamma \to Q\times \Gamma \times \{-1,0,+1\}$ die Übergangsfunktion ist wobei gilt:

1. für alle $p\in Q$ ein $q\in Q$ und $d\in \{0,+1\}$ existieren, so dass $\delta (p,[)=(q,[,d)$ und
2. für alle $a\in \Gamma$ gilt $\delta (q_a,a)=(q_a,a,0)$ und $\delta (q_r,a)=(q_r,a,0)$

$q_s\in Q$ der Anfangszustand
$q_a\in Q$ der akzeptierende Zustand
$q_r\in Q$ der verwerfende Zustand mit $q_a\ne q_r$

WHILE-Programme

Zusammen mit Grammatiken und Sprachen

Die Chomsky-Hierarchy

	Name	Grammatik	Sprache	äquivalent
Typ 0		Jede		Turing Maschine
Typ 1	monoton	$w⟶u\Vert w\Vert \le \Vert u\Vert$		linear beschränkte NTM
Typ 2	Kontextfreie Grammatik	$A⟶w$	Kontextfreie Sprache	Kellerautomat
Typ 3	rechtslinear	$A⟶u$ oder $A⟶uB$	Reguläre Sprache	DEA, NEA, ε-NEA, wort-NEA

siehe:
Sprachklasse

Link to original

Berechenbarkeit / Entscheidbarkeit / Wortproblem

$L_{entscheidbar}=\{L(M)|M\text{ ist TM und entscheidet in endlicher Zeit ob }w\in L(M)\text{ oder }w\notin L(M)\}$

Church-Turing These

Church-Turing These

Die Klasse der Turing-berechenbaren Funktionen stimmt mit der Klasse der intuitiv berechenbaren Funktionen überein.

siehe: entscheidbar

Link to original

Satz von Rice

Für Beweise

P is not trivial when $\exists M,M^{\prime }$ with $M\in P$ and $M\notin P$

P is trivial if $P=\varnothing$ or $P=\{<M>|\text{ any Maschine }M\}$

P is not semantik if $\exists M,M^{\prime }$ with $L(M)=L(M^{\prime })$, $M\in P$ and $M\notin P$

P is semantik if $\forall M,M^{\prime }$ with $L(M)=L(M^{\prime })$ then $M\in P⟺M^{\prime }\in P$

Eine Eigenschaft $\mathcal{P}$ heißt nach oben abgeschlossen, falls für alle semi-entscheidbaren
$L\subset L^{\prime }\subset {\Sigma }^{\ast }$ mit $L\in \mathcal{P}$ auch gilt $L^{\prime }\in P$

semi-entscheidbar / Halteproblem

$L_{\text{semi-entscheidbar}}=\{L(M)|M\text{ ist TM und erkennt in endlicher Zeit wenn }w\in L(M))\}$

Liste aller verwendbaren nicht entschidbaren Probleme

• Halteproblem
• Äquivalenzproblem
• Leerheitsproblem

Liste aller verwendbaren nicht semi entschidbaren Probleme

• Äquivalenzproblem

• Leerheitsproblem

Reduktionen

Definition

Eine Reduktion von $L_1\in {\Sigma }^{\ast }$ auf $L_2\in {\Sigma }^{\ast }$
ist eine (totale)berechenbare Funktion.
$f:{\Sigma }^{\ast }\to {\Sigma }^{\ast }$
so das für alle $W\in {\Sigma }^{\ast }$ gilt:
$L_1\le L_2:=\forall w\in L_1⟺f(w)\in L_2$

Eine Reduktion von $L$ auf $L^{\prime }$ schreibt man als $L\le L^{\prime }$

Wenn $L_1\le L_2$, dann:
$L_1$ (semi) entschidbar $\Leftarrow$ $L_2$ (semi) entschidbar
$L_1$ nicht (semi) entschidbar $\Rightarrow$ $L_2$ nicht (semi) entschidbar
$L_1{\le }_T{L}_2$

Turing-Reduktionen

Definition

$L_1$ ist eine Turing-reduzierbar auf $L_2$ geschrieben ($L_1{\le }_T{L}_2$)
wenn es eine Orakel-Turingmaschinen mit Orakel $L_2$ gibt, die $L_1$ entscheidet.

Wenn $L_1{\le }_T{L}_2$, dann:
$L_1$ entschidbar $\Leftarrow$ $L_2$ entschidbar
$L_1$ nicht entschidbar $\Rightarrow$ $L_2$ nicht entschidbar

Polynomialzeitreduktionen

Laufzeit und Platz-komplexitätsklasen

LogSpace $\subseteq$ NLogSpace $\subseteq$ P-Time $\subseteq$ NP-Time $\subseteq$ P-Space = NP-Space $\subseteq$ Exp-Time

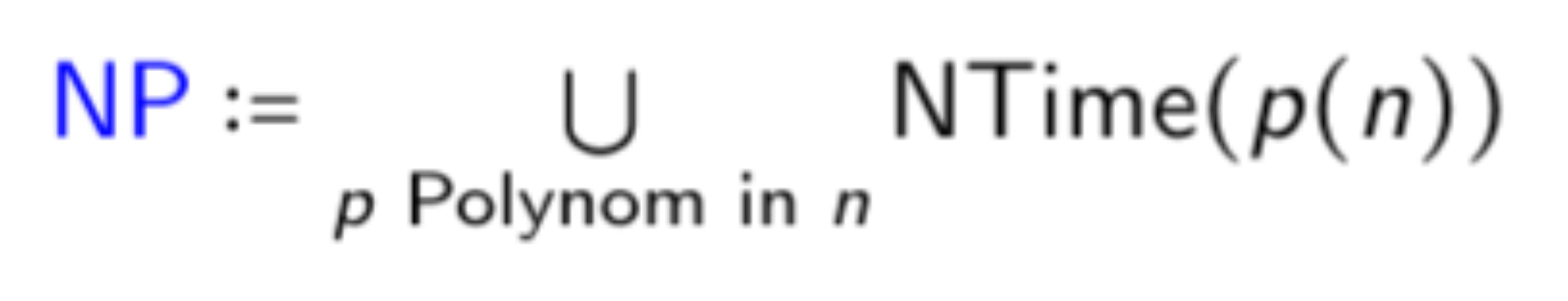
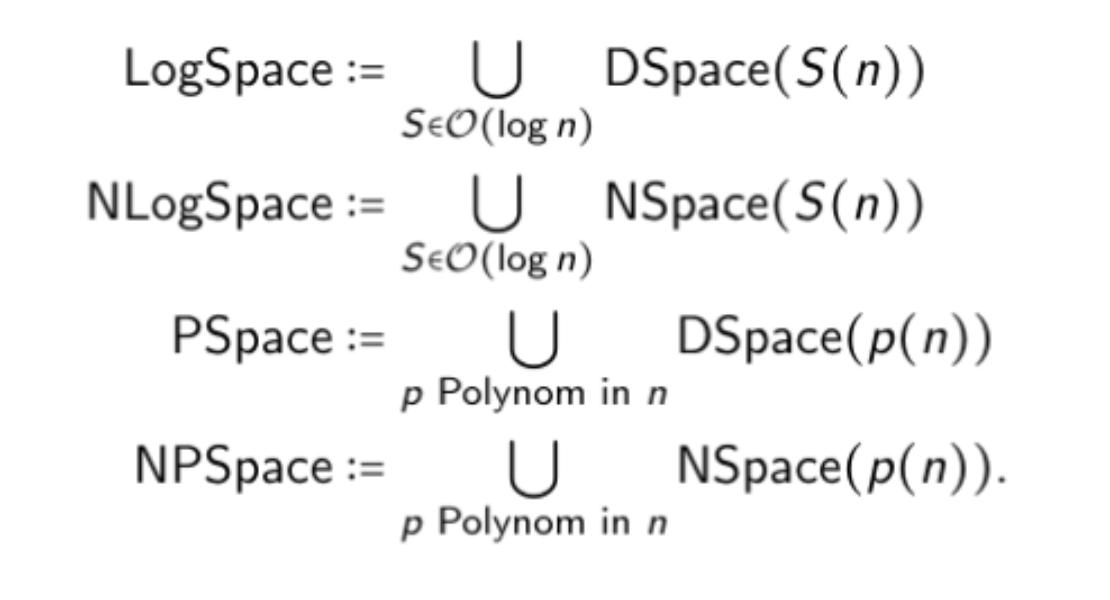
Definition

Eine Sprache $L$ heißt NP-schwer, wenn für alle $L^{\prime }\in NP$ gilt $L^{\prime }{\le }_{p}L$

Definition

$L$ heißt NP-vollständig, wenn $L\in NP$ und $L$ NP-schwer ist.

Für jede NP-vollständige Sprache $L$ gilt: wenn $L\in P$, dann P = NP

Probleme

SAT

Vertex Cover

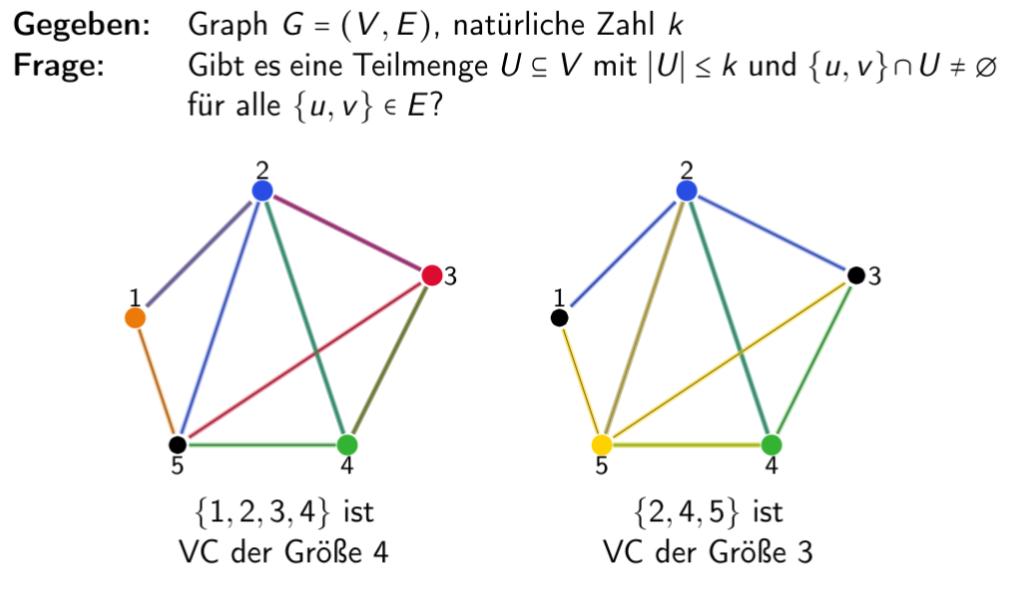
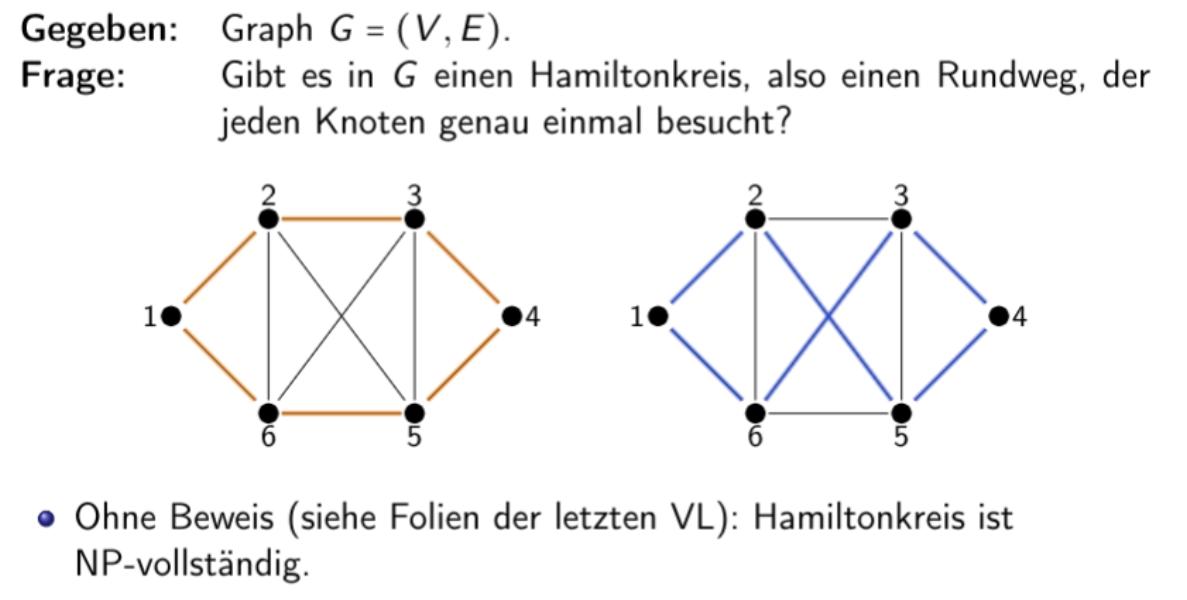
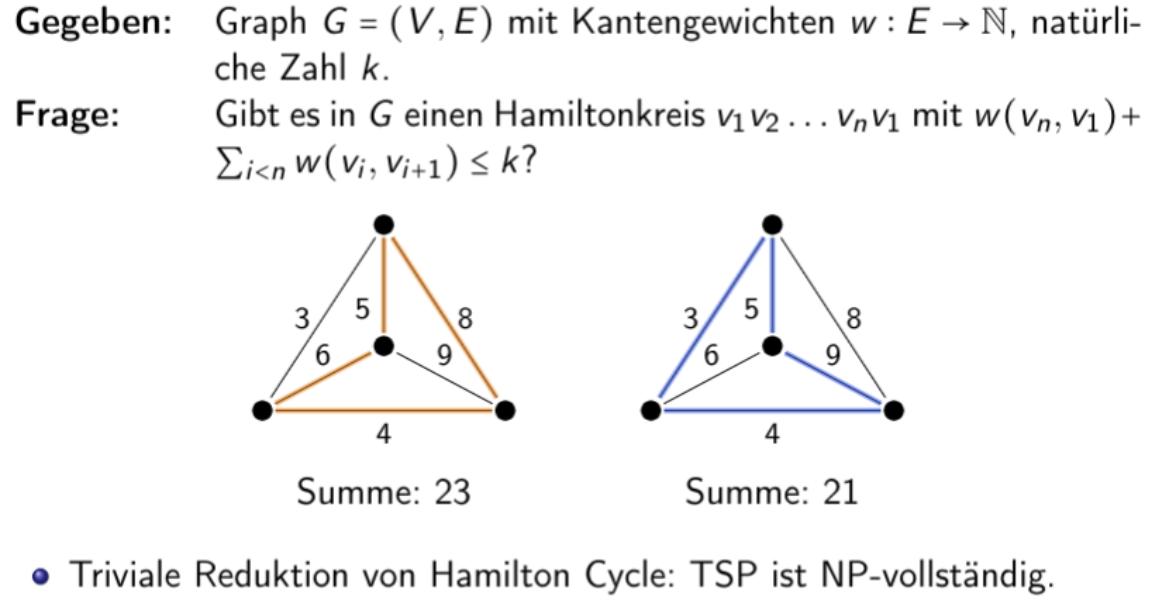
Hamilton Kreis

Clique

Independent Set

Travelling Salesperson Problem