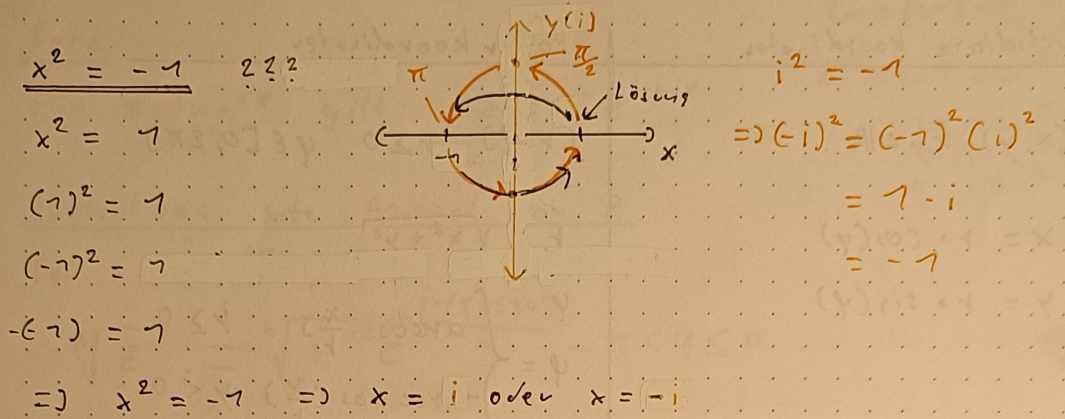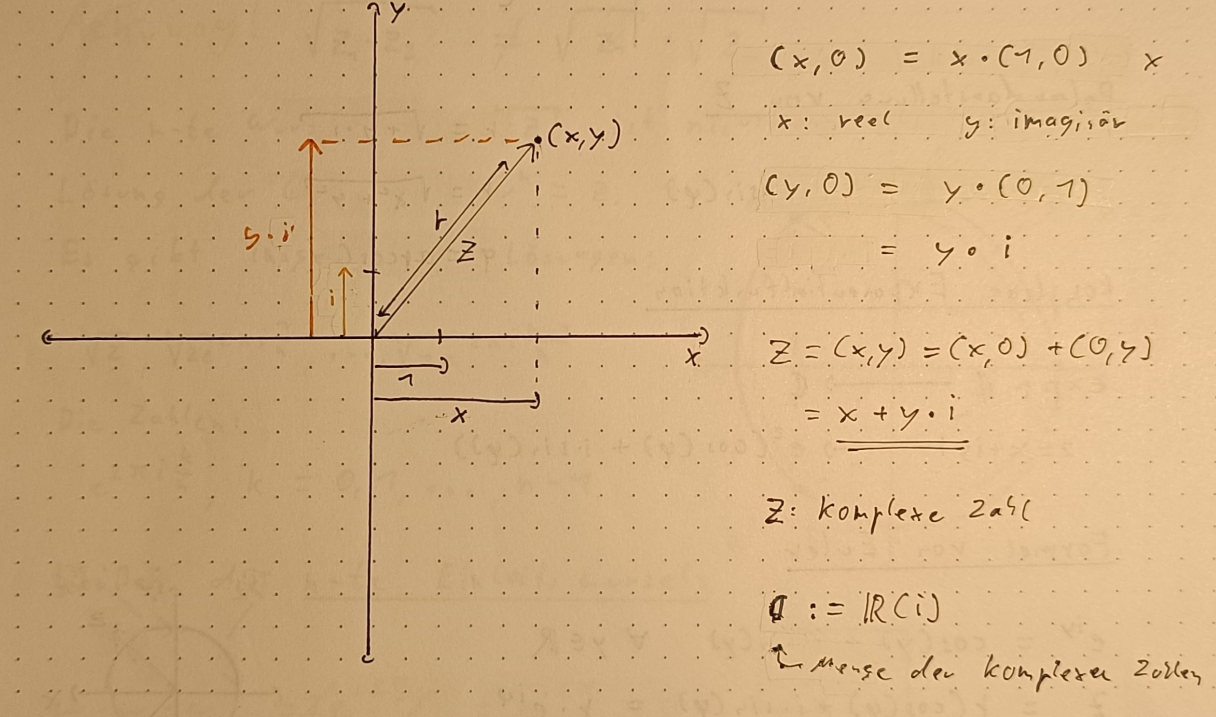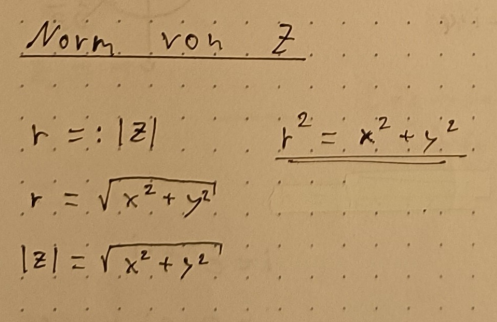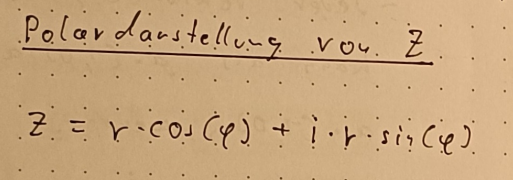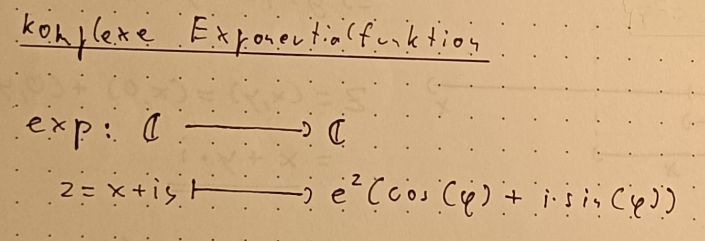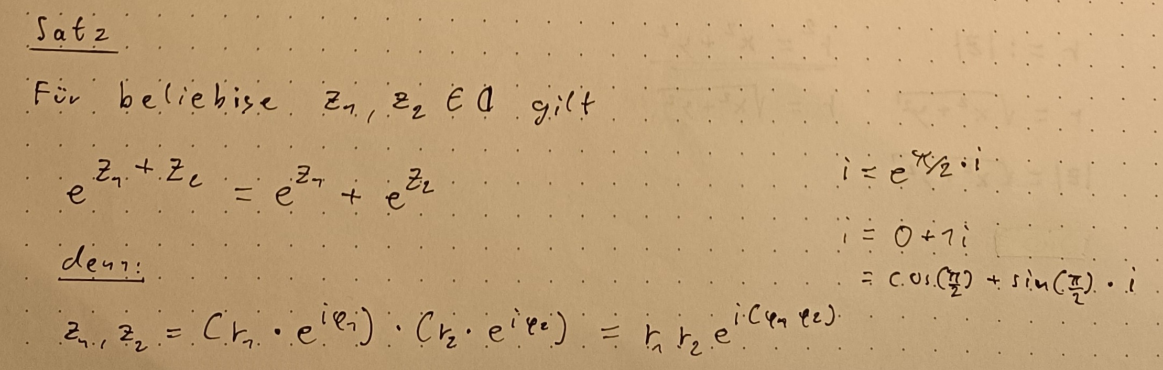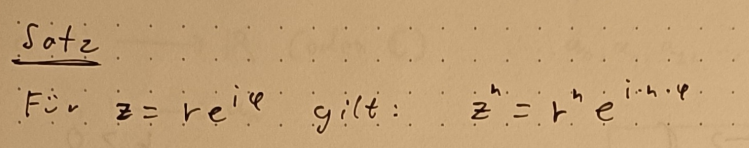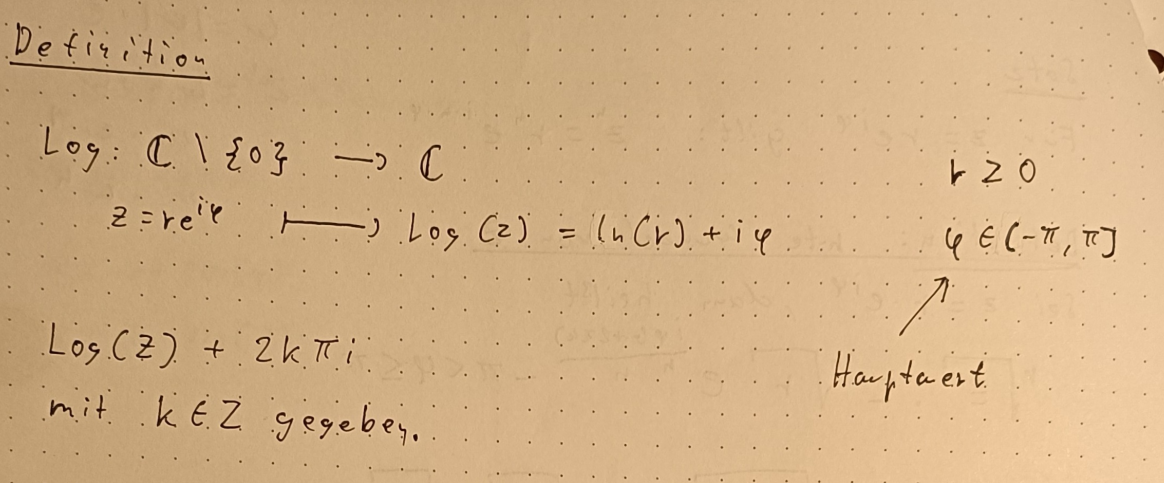Zahlenmengen

$\mathbb{N}\subset {\mathbb{N}}_0\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C}$

Natürliche Zahlen

Die Menge der natürlichen Zahlen  heißt natürlich, weil du mit ihnen Dinge aus der Natur abzählen kannst. Du kannst zum Beispiel die Zahl von Bäumen oder Steinen mit einer natürlichen Zahl angeben. Ihr Mengensymbol ist .
    $\mathbb{N}=\{1;2;3;4;\dots \}$

Ist 0 eine natürliche Zahl? Das wird unter Mathematikern noch diskutiert. Wenn du auf Nummer sicher gehen willst, kannst du die Menge der natürlichen Zahlen mit 0 als aufschreiben.
    ${\mathbb{N}}_0=\{0;1;2;3;4;\dots \}$

In Mat1 enthält $\mathbb{N}$ die 0

Link to original

Ganze Zahlen

Die Menge der ganzen Zahlen  enthält die Zahl 0, alle natürliche Zahlen und ihre Gegenzahlen. Die Gegenzahlen sind die natürlichen Zahlen mit negativem Vorzeichen. Das Symbol der natürlichen Zahlen ist .

    $\mathbb{Z}=\{\dots ;-3;-2;-1;0;1;2;3;\dots \}$

Link to original

Rationale Zahlen

Die Menge der rationalen Zahlen  enthält alle ganzen Zahlen und Brüche aus ganzen Zahlen. Das sind Brüche, die im Nenner und im Zähler eine ganze Zahl stehen haben. Die rationalen Zahlen werden mit einem abgekürzt. Nicht vergessen: Du kannst die Brüche auch als Dezimalzahlen schreiben $\frac{1}{3}=0,\bar{3}$

    $\mathbb{Q}=\{\dots ;-2\frac{1}{4};-\frac{7}{8};0;1;0,\bar{3};\dots \}$

Link to original

Irrationale Zahlen

Die Menge der irrationalen Zahlen  sind alle Zahlen, die nicht rational sind. Sie lassen sich also nicht als ein Bruch ganzer Zahlen schreiben. Irrationale Zahlen sind nicht periodisch und nicht abbrechend. Das bedeutet, sie haben unendlich viele Nachkommastellen, die sich nicht mit einem regelmäßigen Muster wiederholen. Das ist zum Beispiel bei pi oder der eulerschen Zahl e der Fall. Das Symbol der irrationalen Zahlen ist .

   $\mathbb{I}=\{\dots ;-\sqrt{2};\mathrm{e};\pi ;\dots \}$

Link to original

Reelle Zahlen

Die Menge der reellen Zahlen  besteht aus den rationalen Zahlen und den irrationalen Zahlen. Hier musst du auf die Rechtschreibung achten (reelle Zahl, nicht reele Zahl oder reele Zahlen).  Die reellen Zahlen werden mit einem abgekürzt.
$\mathbb{R}=\mathbb{Q}\cup \mathbb{I}=\{\dots ;-2\frac{1}{4};-\sqrt{2};-\frac{7}{8};0;1;0,\bar{3};\mathrm{e};\pi ;\dots \}$

Link to original

Komplexe Zahlen

Definition

Die Menge der komplexen Zahlen besteht aus den reellen Zahlen und den imaginären Zahlen . Das Symbol der komplexen Zahlen ist ein .

Komplexe Zahlen haben die Form . a und b sind reelle Zahlen. Sie bestehen aus einem Realteil a (einer reellen Zahl) und einem Imaginärteil bi (einer imaginären Zahl). Mit den komplexen Zahlen kannst du negative Wurzeln berechnen berechnen, denn für die imaginäre Einheit i gilt: .

$\mathbb{C}=\{\dots ;{\mathrm{e}}^{\mathrm{i}\pi };-5+2\mathrm{i};0;\sqrt{-1};3;4;\dots \}$

Aus Mat 2

siehe auch:
Wurzel komplexe Zahlen
Polarkoordinaten
Eulersche Formel

Link to original