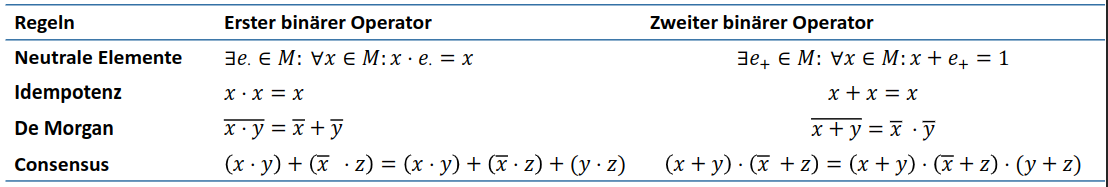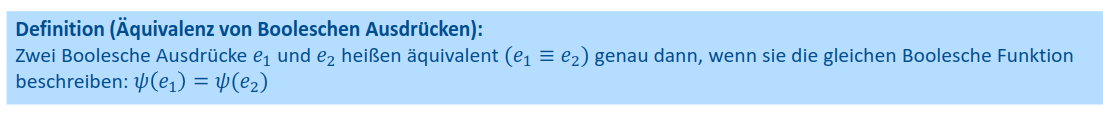TI1 VL 07

kap7-1.pdf

Boolische Funktionen

Definitions Bereiche

Definition (Boolesche Funktion):

Beispiel:

Sei 𝑛 = 2 und 𝑚 = 1.
Dann ist 𝑓: 𝔹2 → 𝔹
mit 𝑓 (0,0) = 𝑓 (1,1) = 0
und 𝑓 (0,1) = 𝑓 (1,0) = 1
eine Boolesche Funktion in
zwei Variablen.

Definition (partielle Boolesche Funktion):

Definition (Erfüllbarkeitsmenge):

𝑂𝑁( 𝑓 ) ≔ {𝛼 ∈ 𝔹𝑛|𝑓 𝛼 = 1}

Definition (Nichterfüllbarkeitsmenge):

𝑂𝐹𝐹( 𝑓 )≔ {𝛼 ∈ 𝔹𝑛|𝑓 𝛼 = 0}

Definition (Definitionsbereich):

𝑑𝑒𝑓( 𝑓 ) ≔ {𝛼 ∈ 𝔹𝑛 | 𝑓 𝛼 𝑑𝑒𝑓𝑖𝑛𝑖𝑒𝑟𝑡 }

Definition („don‘t-care“-Bereich):

DC( 𝑓 )≔ {𝛼 ∈ 𝔹 𝑛 | 𝑓 𝛼 𝑛𝑖𝑐ℎ𝑡 𝑑𝑒𝑓𝑖𝑛𝑖𝑒𝑟𝑡}

Relation

kleiner

𝑓 heißt kleiner als 𝑔, wenn 𝑓 𝛼 ≤ 𝑔 𝛼 ∀𝛼 ∈ 𝔹𝑛

siehe auch
Logik

Link to original

Boolesche Algebra

Sein $\cdot$ und + sind zwei belibige binäre Operatoren.

Abgeleitete Rechenregeln

Dualitätsprinzip

Sei 𝑝 dual die aus 𝑝 abgeleitete duale Gleichung. Diese geht durch das gleichzeitige Vertauschen der binären Operatoren
sowie der neutralen Elemente aus 𝑝 hervor. Ist 𝑝 gültig, so ist auch 𝑝𝑑𝑢𝑎𝑙 gültig.

⇒ Wenn man alle operatoren und einsen und nullen tauscht erhält man das gleiche.

Boolesche Ausdrücke

Interpretation Boolescher Ausdrücke

Spezielle Boolesche Ausdrücke (Auswendig lernen)

Literale

• boolische Ausdrücke ($x_j$ oder $\overline{x_j}$)

Monome

• Konjunktion von Literalen
• Jedes Literal kommt nur einmal vor. (Nur positiv oder negativ)
  $A:=x_1\wedge x_2\wedge ...\wedge x_n$

Minterme (vollständiges Monom):

• enthält jedes Literal.

Polynome

Polynome sind eine Disjunktion von paarweise verschiedenen Monomen
$P:=A_1\vee A_2\vee ...\vee A_n$

Vollständige Polynome

bestehen nur aus vollständigen Monomen

Normalformen

Disjunktive Normalformen einer Booleschen Funktion 𝑓 sind Polynome von 𝑓

Kanonische Disjunktive Normalformen

einer Booleschen Funktion 𝑓 sind vollständige Polynome von 𝑓

Satz (Eindeutigkeit der KDNF):

Die kanonische disjunktive Normalform einer Boolschen Funktion 𝑓 ist eindeutig.

Boolesche Funktionen & Boolesche Ausdrücke

Link to original