20221028_TH_M1-Skript_v02-7.pdf
Dr. Tim Haga
erreichen:
im Büro: MZH 7172
+49 421 218-63683
timhaga@uni-bremen.de
nicht Stud.ip → E-Mail
Inhalte:
- Logik
- Mengen
- Relationen
- Kombinatorik
- Algebra
- Geometrie
wöchentliche Präsenzaufagben
Kern der Mathematik
In der Mathematik geht es um Folgende
- Wir geben uns ein System von Axiomen vor.
- Daraus viele wahre Aussagen ableiten.
Beispiel
An der Uni Bremen soll der eneue Multi-Kombi-Bachelor eigeführt werden.
Der Studiengang soll sich aus
Jeder Student belegt mindestens ein Fach
Zwei verschiedene Studenten belegen immer genua ein gemiensames Fach
Zu jedem Fach gibt es genau ein anderes Fach
Aussagenformen
Eine Aussageform ist ein Ausdruck in Variablen der zu einer Aussage wird wenn alle darin vorkommenden Variablen durch konkrete Objekte ersetzt werden. Diese Objekte müssen aus einer geeigneten Grundgesamtheit kommen.
x ist ohne Rest durch 7 teilbar. Eine geeignete Grundgesamtheit für x sind z. B. die natürliche Zahlen. • y = 4x + 5. Geeignete Grundgesamtheiten für x und y sind z. B. die reellen Zahlen.
Sprachen
Altagssprache nicht präzise genug.
daher formale Sprachen (Sufe 1)
¬ (für „nicht“),
∧ (für „und“),
∨ (für „oder“),
→ (für „wenn – dann“), ↔ (für „genau dann wenn“),
∀ (für „für alle“), ∃ (für „es gibt“)
= (als Gleichheitszeichen).
Außerdem nehmen wir Variablen (für vorkommende Objekte, Strukturen, usw.) und Klammern als Hilfsymbole dazu.
Negation von Aussagen
Logisches Nicht
Link to originalAussage A: Die Zahl 7 ist gerade.
Negation von A: Die Zahl 7 ist ungeradeAussage B: Alle Schafe sind schwarz.
Negation von B: Nicht alle Schafe sind schwarz.Aussage: Es gibt eine reelle Zahl x für die gilt x > 7.
Negation: Für alle reellen Zahlen x gilt: x ≤ 7.Aussage: Für alle reellen Zahlen x gilt: x 2 ≥ 0.
Link to original
Negation: Es gibt eine reelle Zahl x für die gilt: x 2 < 0.
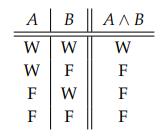
Konjunktion von Aussagen (und)
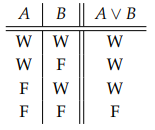
Disjunktion von Aussagen (Logisches Oder)
Wenn-Dann-Verknüpfung oder Subjunktion zweier Aussagen