Gruppentheorie

up:: Mat1 MOC

Transclude of algebraische-Struckturen-0.canvas

Verknüpfung

Definition

Sei $M$ eine nichtleere Menge. Eine Verknüpfung $\ast$ auf $M$ ist eine Abbildung

\begin{array}{c, c, l} *: & M \times M & \longrightarrow & M \\ & (a,b) & \longmapsto & a * b \end{array} Link to original

Gruppe

Übersicht

Name	abgeschlossen	assoziativ	neutral Element	inverses neutral Element	kommutativ
Magma	x
Halbgruppe	x	x
Monoid	x	x	x
Gruppe	x	x	x	x
abelsche Gruppe	x	x	x	x	x

Definition Gruppe

• Eine Verknüpfung zwischen einer Menge und einem Operator.
  z.B: $G(\mathbb{Z},+)$ also Menge $\mathbb{Z}$ mit $+$.

• Die Menge darf nich leer sein.

• Die Gruppen ist abgeschlossen.
  $\forall a,b\in G\exists c\in Ga\ast b=c$

• Für Gruppen gilt das

  Assoziativgesetz

  $(a\ast b)\ast c=a\ast (b\ast c)$

  Link to original

• Neutrales Element: Es gibt ein $e\in G$ sodass $e\ast a=a\ast e=a$ ist.

  • links neutral: Wenn nur $e\ast a=a$
  • rechts neutral: Wenn nur $a\ast e=a$
  • komplett neutral: Wenn nur $e\ast a=a\ast e=a$
    z.B: $0$ für $\mathbb{Z}$

• Inverses Element: Für alle $a\in G$ gibt es ein $a^{\prime }\in G$ sodass $a\ast a^{\prime }=a^{\prime }\ast a=e$ ist.
  z.B: $-8$ für $8$
  statt $a^{\prime }$ schreibt man gerne $a^{-1}$

Untergruppe

Definition

Ist $(G,\ast )$ eine Gruppe und $U\subseteq G$ eine Teilmenge von $G$.
Dann heißt $U$ Untergruppe von $G$, falls $(U,\ast )$ selbst wieder eine Gruppe ist.
Wir schreiben: $U<G$

Link to original

siehe auch: Restklassengruppen-Modulo

Rechnen mit Gruppen:

$\forall g,h\in G$ gilt:

$(g^{-1}{)}^{-1}=g$
$(g\ast h{)}^{-1}=h^{-1}\ast g^{-1}$
$k=g\ast h$

Kürzungsregeln

$ac=bc\Rightarrow a=b$
$ca=cb\Rightarrow a=b$

$\exists !x\in G:g\ast x=h$
$\exists !y\in G:y\ast g=h$

Link to original

Verknüpfungstabelle

Homomorphismen

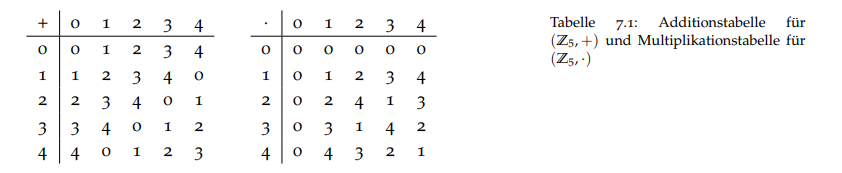
Ring

Definition

Sein $R$ eine Menge mit zwei assoziativen Verknüpfungen $+$ und $\cdot$ auf $K$. Dann heißt $(R,+,\cdot )$ Ring, falls:

• $(R,+)$ eine abelsche Gruppe ist

• und für $+$, die Distributivgesetze gelten.

• Ein Ring heißt kommutativ, falls $\cdot$ eine kommutative Verknüpfung ist.

• Gilt $\forall a,b\in R:ab=0\Rightarrow a=0\vee b=0$, so heißt der Ring nullteilerfrei.

• Gibt es ein neutrales Element bezüglich $\cdot$ (oft wir dieses $1$ gennant), so heißt $R$ Ring mit Eins.

Einheitsgruppe

Definition

Ist $(R,+,\cdot )$ ein Ring mit Eins. Ein Element $a\in R$ heißt Einheit, wenn es ein $b\in R$ gibt, so dass gilt: $ab=ba=1$.

Einheiten sind also die multiplikativ invertierbaren Elemente von $R$.
Wir bezeichnen die Menge der Einheiten von $R$ mit $R^{\ast }$.

Link to original

Link to original

Körper

Definition

Ein Körper ist eine algebraische Strucktur $(K,+,\cdot )$

• $(K,+)$ abelsche Gruppe (Neutral Element 0)
• $(K,\cdot )$ abelsche Gruppe (Neutral Element 1)
• Es gelten die Distributivgesetz

Charakteristik von einem Körper

Link to original